Grundlagen

Zuvor haben wir lineare Gleichungen gesehen und wie in ihnen die Variable (normalerweise x) nicht um einen Grad größer als 1 angehoben wird.
Eine Gleichung kann mehr Variablen als x umfassen, beispielsweise y.
br>
Beispiel: x+y=1.

Die Gleichung im Beispiel ist linear, da keine der Variablen auf eine Potenz größer als 1 erhöht wird.

An Gleichung mit x und y kann grafisch dargestellt werden. Dazu betrachten wir alle Punkte der kartesischen Ebene (x,y), die diese treffen.

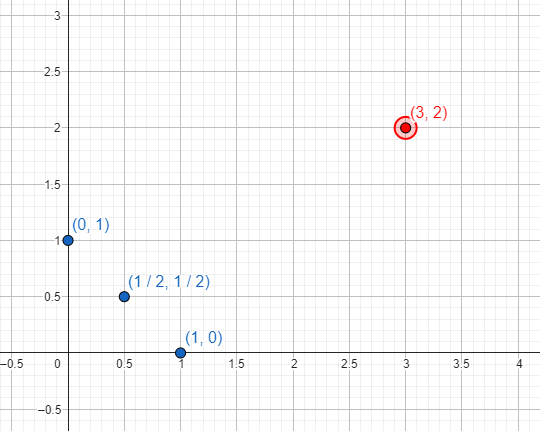
Beispiel: die Punkte (0,1), (1/2,1/2 ) und (1,0) entsprechen unter anderem der Gleichung „x+y=1“. (3,2) erfüllt es jedoch nicht, sodass es nicht im Diagramm der Gleichung enthalten wäre.


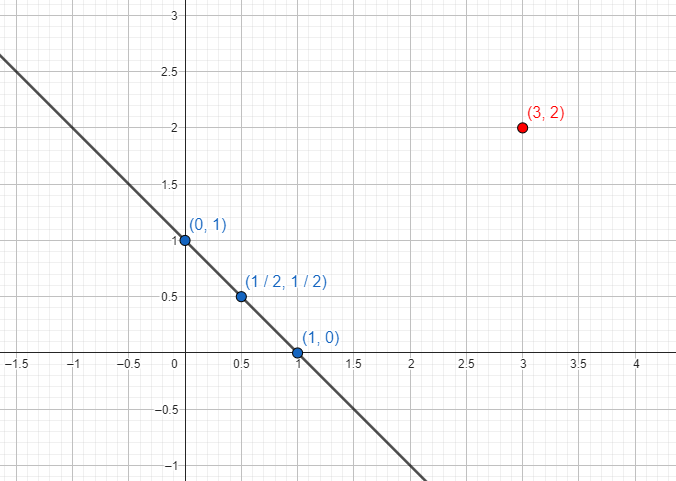
Der Graph, der linearen Gleichungen entspricht, ist der einer Linie, die durch alle Punkte verläuft, die die Gleichung erfüllen. Um eine Linie zu bestimmen, genügt es, zwei darauf liegende Punkte anzugeben (drei erscheinen unten):



Ein System aus zwei linearen Gleichungen ist ein Satz von zwei linearen Gleichungen mit x und y, in denen jede von ihnen eine Linie darstellt, wie wir gerade gesehen haben. Um das System zu lösen, müssen Sie die Werte von x und y finden, die dafür sorgen, dass die beiden Gleichungen gleichzeitig erfüllt sind.

Beispiel: Wie wir zuvor gesehen haben, gibt es mehrere Punkte, die erfüllt sind die Gleichung „x+y=1“. Es gibt auch mehrere Punkte, die „x-y=1“ erfüllen. Allerdings erfüllt nur der Punkt (1,0) beides. Daher ist „x=1, y=0“ die Lösung des Systems, das durch diese beiden Gleichungen gebildet wird.

Um ein System grafisch zu lösen, müssen wir jede Gleichung berücksichtigen stellt eine Linie dar. Die Lösung ist der Punkt, an dem sich beide Linien schneiden.

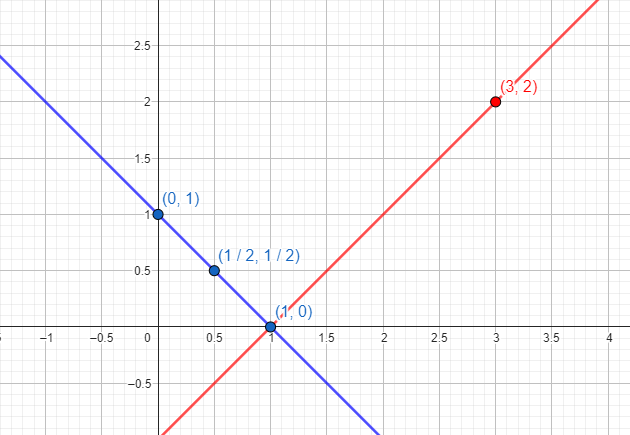
Beispiel: Die aus „x+y=1“ und „x-y=1“ erhaltenen Linien erscheinen in der Zeichnung unten. Wir sehen, dass der einzige Punkt, an dem sie sich schneiden, (1,0) ist. Daher ist „x=1, y=0“ die Lösung des Systems.