Basics
Completion requirements
Previously we have seen linear equations, and how in them the variable (usually x) is not raised to any degree greater than 1.
An equation can involve more variables than x, such as y.
br>
Example: x+y=1.
The equation in the example is linear because none of the variables is raised to a power greater than 1.
An equation involving x and y can be represented graphically. To do this, we look at all the points of the Cartesian plane (x,y) that meet it.
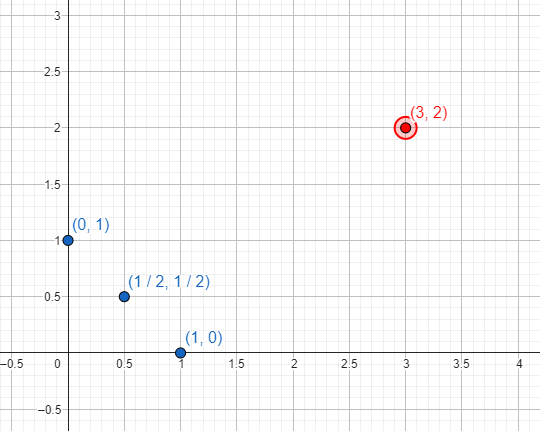
Example: the points (0,1), (1/2,1/2) and (1,0), among others, do comply with the equation "x+y=1". However, (3,2) does not satisfy it, so it would not be on the graph of the equation.
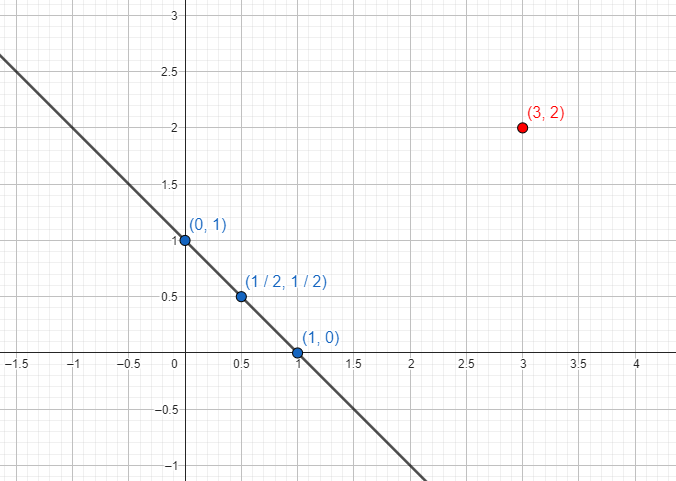
The graph that corresponds to linear equations is that of a line that passes through all the points that satisfy the equation. To determine a line, it is enough to indicate two points that are on it (three appear below):
A system of two linear equations is a set of two linear equations involving x and y, in which each of them represents a line as we just saw. To solve the system you have to find the values of x and y that make the two equations satisfy at the same time.
Example: as we have seen before, there are several points that satisfy the equation "x+y=1". There are also several points that satisfy "x-y=1". However, only the point (1,0) fulfills both. Therefore, "x=1, y=0" is the solution of the system formed by these two equations.
To solve a system graphically, we must take into account that Each equation represents a line. The solution is the point at which both lines intersect.
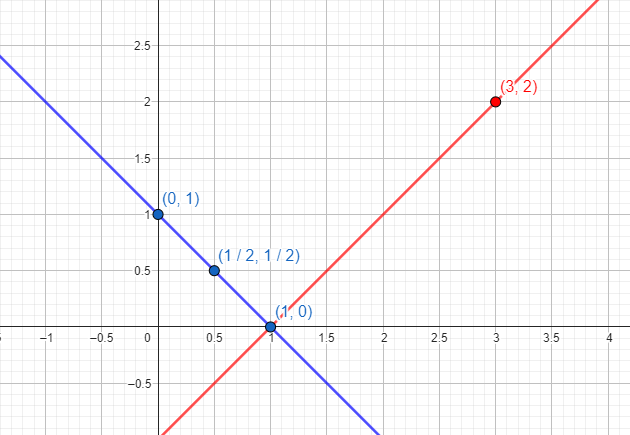
Example: the lines obtained from "x+y=1" and "x-y=1" appear in the drawing below. We see that the only point where they intersect is (1,0). Therefore, "x=1, y=0" is the solution of the system.
An equation can involve more variables than x, such as y.
br>
Example: x+y=1.
The equation in the example is linear because none of the variables is raised to a power greater than 1.
An equation involving x and y can be represented graphically. To do this, we look at all the points of the Cartesian plane (x,y) that meet it.
Example: the points (0,1), (1/2,1/2) and (1,0), among others, do comply with the equation "x+y=1". However, (3,2) does not satisfy it, so it would not be on the graph of the equation.

The graph that corresponds to linear equations is that of a line that passes through all the points that satisfy the equation. To determine a line, it is enough to indicate two points that are on it (three appear below):

A system of two linear equations is a set of two linear equations involving x and y, in which each of them represents a line as we just saw. To solve the system you have to find the values of x and y that make the two equations satisfy at the same time.
Example: as we have seen before, there are several points that satisfy the equation "x+y=1". There are also several points that satisfy "x-y=1". However, only the point (1,0) fulfills both. Therefore, "x=1, y=0" is the solution of the system formed by these two equations.
To solve a system graphically, we must take into account that Each equation represents a line. The solution is the point at which both lines intersect.
Example: the lines obtained from "x+y=1" and "x-y=1" appear in the drawing below. We see that the only point where they intersect is (1,0). Therefore, "x=1, y=0" is the solution of the system.


Last modified: Friday, 19 July 2024, 2:56 PM