Conceptos básicos
Requisitos de finalización
Previously we have seen linear equations, and how in them the variable (usually x) is not raised to any degree greater than 1.
An equation can involve more variables than x, such as y.
br>
Example: x+y=1.
The equation in the example is linear because none of the variables is raised to a power greater than 1.
An equation involving x and y can be represented graphically. To do this, we look at all the points of the Cartesian plane (x,y) that meet it.
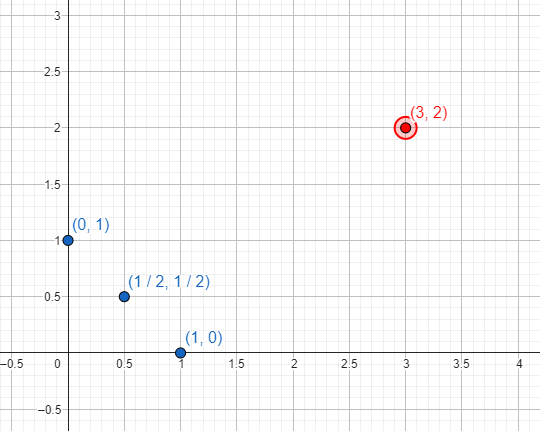
Example: the points (0,1), (1/2,1/2) and (1,0), among others, do comply with the equation "x+y=1". However, (3,2) does not satisfy it, so it would not be on the graph of the equation.
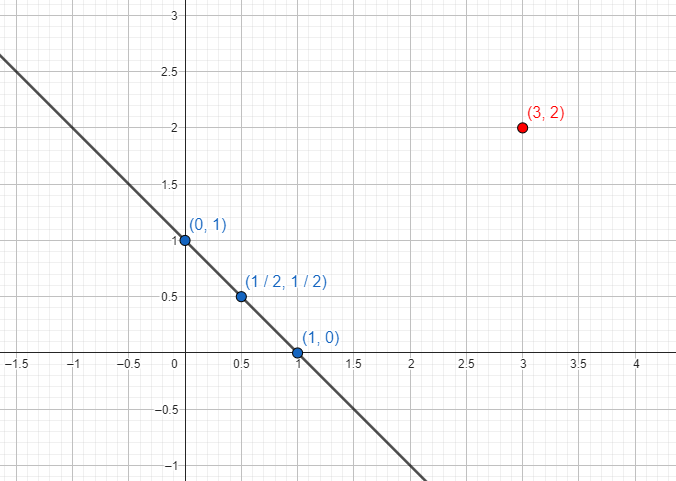
The graph that corresponds to linear equations is that of a line that passes through all the points that satisfy the equation. To determine a line, it is enough to indicate two points that are on it (three appear below):
A system of two linear equations is a set of two linear equations involving x and y, in which each of them represents a line as we just saw. To solve the system you have to find the values of x and y that make the two equations satisfy at the same time.
Example: as we have seen before, there are several points that satisfy the equation "x+y=1". There are also several points that satisfy "x-y=1". However, only the point (1,0) fulfills both. Therefore, "x=1, y=0" is the solution of the system formed by these two equations.
To solve a system graphically, we must take into account that Each equation represents a line. The solution is the point at which both lines intersect.
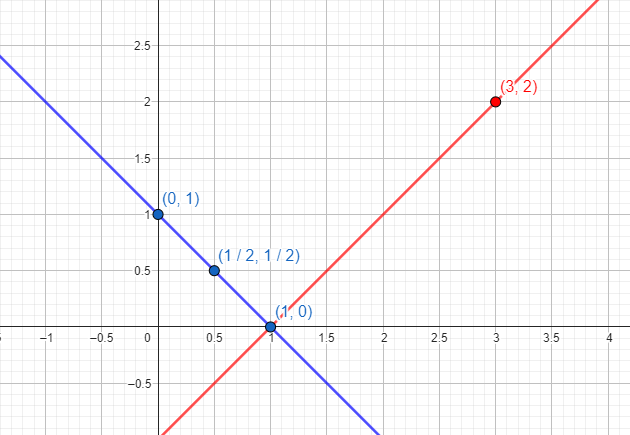
Example: the lines obtained from "x+y=1" and "x-y=1" appear in the drawing below. We see that the only point where they intersect is (1,0). Therefore, "x=1, y=0" is the solution of the system.
An equation can involve more variables than x, such as y.
br>
Example: x+y=1.
The equation in the example is linear because none of the variables is raised to a power greater than 1.
An equation involving x and y can be represented graphically. To do this, we look at all the points of the Cartesian plane (x,y) that meet it.
Example: the points (0,1), (1/2,1/2) and (1,0), among others, do comply with the equation "x+y=1". However, (3,2) does not satisfy it, so it would not be on the graph of the equation.

The graph that corresponds to linear equations is that of a line that passes through all the points that satisfy the equation. To determine a line, it is enough to indicate two points that are on it (three appear below):

A system of two linear equations is a set of two linear equations involving x and y, in which each of them represents a line as we just saw. To solve the system you have to find the values of x and y that make the two equations satisfy at the same time.
Example: as we have seen before, there are several points that satisfy the equation "x+y=1". There are also several points that satisfy "x-y=1". However, only the point (1,0) fulfills both. Therefore, "x=1, y=0" is the solution of the system formed by these two equations.
To solve a system graphically, we must take into account that Each equation represents a line. The solution is the point at which both lines intersect.
Example: the lines obtained from "x+y=1" and "x-y=1" appear in the drawing below. We see that the only point where they intersect is (1,0). Therefore, "x=1, y=0" is the solution of the system.

Anteriormente hemos visto ecuaciones lineales, y cómo en ellas la variable (por lo general, la x) no está elevada a ningún grado mayor que 1.
Una ecuación puede involucrar a más variables aparte de la x, como la y.
Ejemplo: x+y=1.
La ecuación del ejemplo es lineal porque ninguna de las variables está elevada a potencia mayor que 1.
Una ecuación que involucra a la x y a la y puede ser representada de forma gráfica. Para ello, nos fijamos en todos los puntos del plano cartesiano (x,y) que la cumplen.
Ejemplo: los puntos (0,1), (1/2,1/2) y (1,0), entre otros, sí cumplen la ecuación "x+y=1". Sin embargo, el (3,2) no la cumple, así que no estaría en la gráfica de la ecuación.

La gráfica que corresponde a ecuaciones lineales es la de una recta que pasa por todos los puntos que cumplan la ecuación. Para determinar una recta, es suficiente con indicar dos puntos que se encuentren en ella (abajo aparecen tres):

Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones lineales que involucran x e y, en las que cada una de ellas representa una recta como acabamos de ver. Para resolver el sistema hay que encontrar los valores de la x y de la y que hagan que las dos ecuaciones se cumplan a la vez.
Ejemplo: como hemos visto antes, hay varios puntos que cumplen la ecuación "x+y=1". También hay varios puntos que cumplen "x-y=1". Sin embargo, sólo el punto (1,0) cumple ambas. Por lo tanto, "x=1, y=0" es la solución del sistema formado por estas dos ecuaciones.
Para resolver un sistema de forma gráfica hay que tener en cuenta que cada ecuación representa una recta. La solución es el punto en el que ambas rectas se cortan.
Ejemplo: las rectas que se obtienen de "x+y=1" y "x-y=1" aparecen en el dibujo de debajo. Vemos que el único punto en el que se cortan es el (1,0). Por lo tanto, "x=1, y=0" es la solución del sistema.

Una ecuación puede involucrar a más variables aparte de la x, como la y.
Ejemplo: x+y=1.
La ecuación del ejemplo es lineal porque ninguna de las variables está elevada a potencia mayor que 1.
Una ecuación que involucra a la x y a la y puede ser representada de forma gráfica. Para ello, nos fijamos en todos los puntos del plano cartesiano (x,y) que la cumplen.
Ejemplo: los puntos (0,1), (1/2,1/2) y (1,0), entre otros, sí cumplen la ecuación "x+y=1". Sin embargo, el (3,2) no la cumple, así que no estaría en la gráfica de la ecuación.

La gráfica que corresponde a ecuaciones lineales es la de una recta que pasa por todos los puntos que cumplan la ecuación. Para determinar una recta, es suficiente con indicar dos puntos que se encuentren en ella (abajo aparecen tres):

Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones lineales que involucran x e y, en las que cada una de ellas representa una recta como acabamos de ver. Para resolver el sistema hay que encontrar los valores de la x y de la y que hagan que las dos ecuaciones se cumplan a la vez.
Ejemplo: como hemos visto antes, hay varios puntos que cumplen la ecuación "x+y=1". También hay varios puntos que cumplen "x-y=1". Sin embargo, sólo el punto (1,0) cumple ambas. Por lo tanto, "x=1, y=0" es la solución del sistema formado por estas dos ecuaciones.
Para resolver un sistema de forma gráfica hay que tener en cuenta que cada ecuación representa una recta. La solución es el punto en el que ambas rectas se cortan.
Ejemplo: las rectas que se obtienen de "x+y=1" y "x-y=1" aparecen en el dibujo de debajo. Vemos que el único punto en el que se cortan es el (1,0). Por lo tanto, "x=1, y=0" es la solución del sistema.

Última modificación: viernes, 19 de julio de 2024, 14:56