Try
Kursthemen
-
Dieser Kurs ist Teil einer Reihe von Plattformen, auf denen Sie die Projektergebnisse des Erasmus+-Projekts AuthOMath zu erkunden können:
- Klicken Sie Inform für ausführliche Informationen über die Ziele, Aktivitäten und Beteiligten des Projekts AuthOMath.
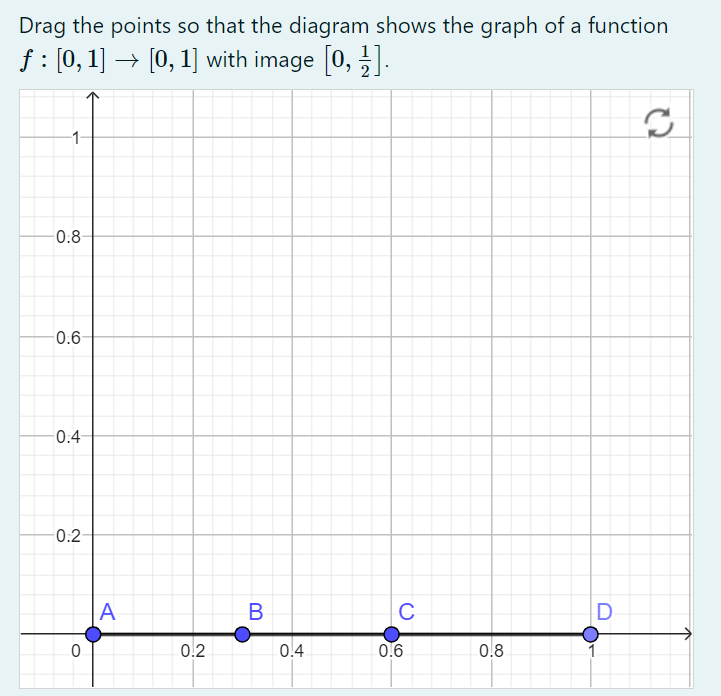
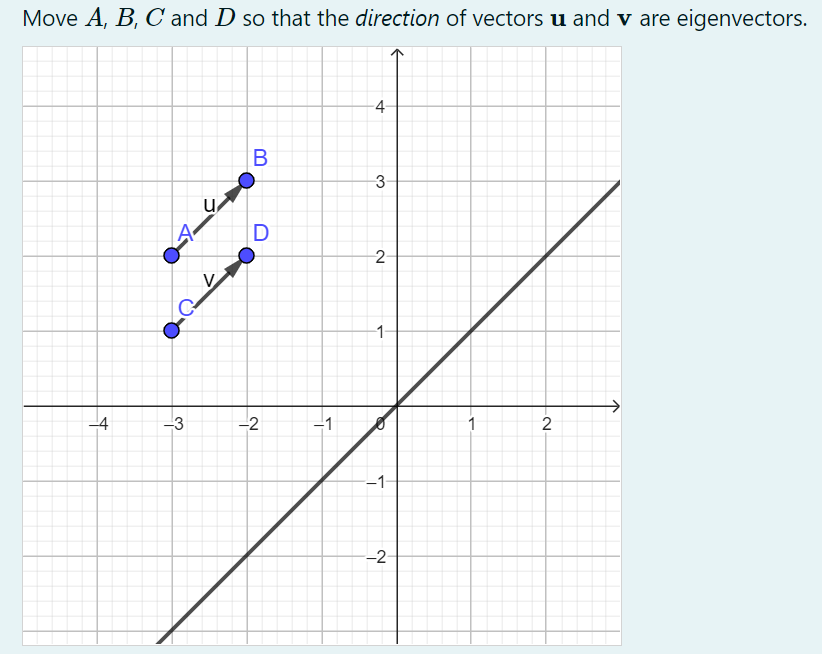
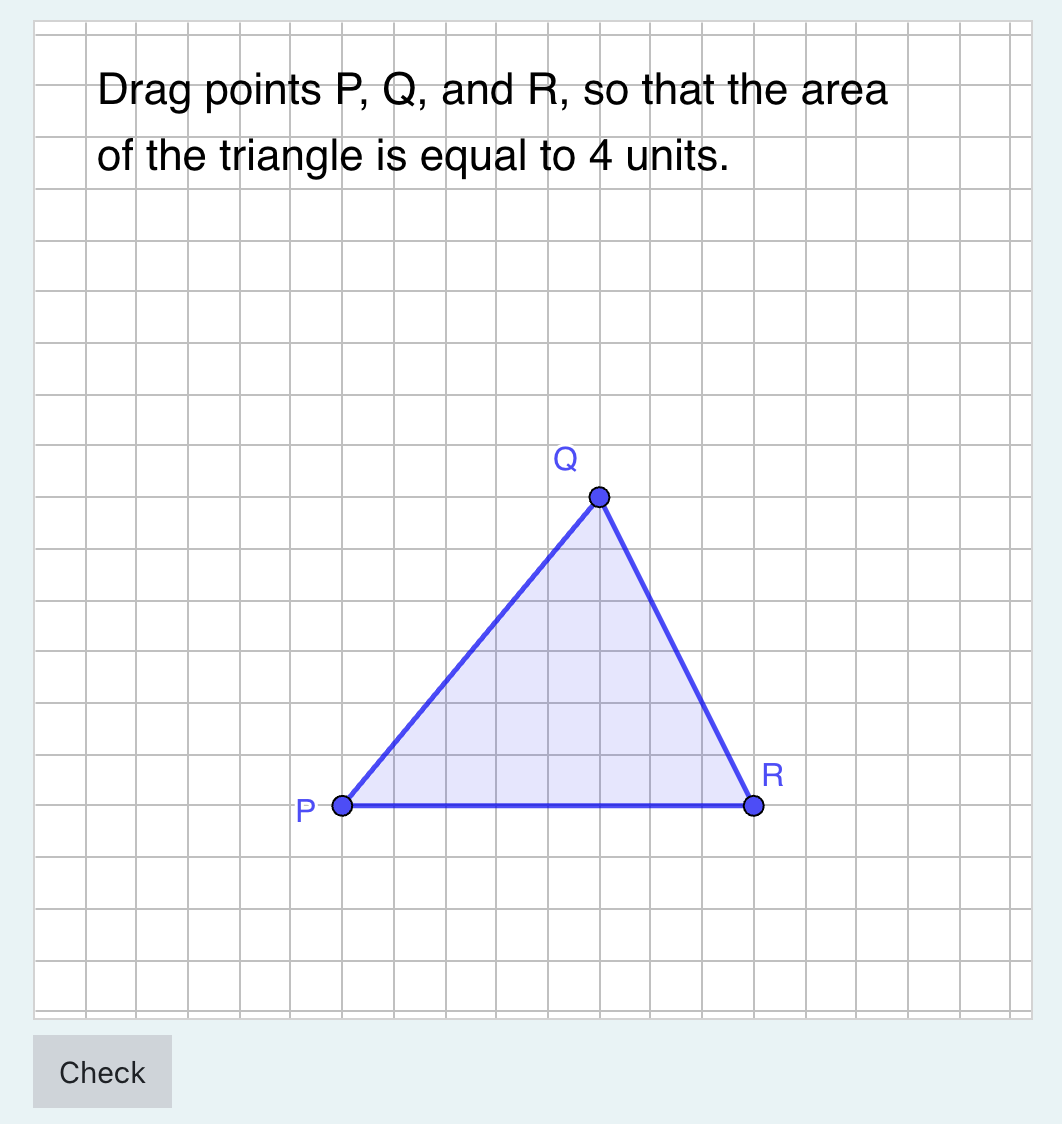
- Bleiben Sie hier auf Try um digitale Mathematikaufgaben auszuprobieren, die mit AuthOMath erstellt wurden.
- Klicken Sie Tinker, um Ihre erste eigene digitale Mathematikaufgabe zu programmieren.
- Warten Sie auf Use, eine Plattform für den Einsatz in der Ausbildung von Mathematiklehrkräften.
- Klicken Sie auf Create um zu erfahren, wie Sie Ihren eigenen STACK-Server aufsetzen können, um Lernmaterialien für Ihre Klassen zu erstellen.
Jede Frage wird zuerst mit Kommentaren zu den didaktischen Überlegungen vorgestellt, die hier zum Einsatz von STACK und GeoGebra geführt haben; dann folgt ein Test, bei dem man die Fragen der Partner ausprobieren kann.
Unten finden Sie vier Abschnitte, jeweils mit Fragen von einem der vier Partner des Projekts AuthOMath. -
-
Aufgabe 1 : Addition von Brüchen
Bei der Beabeitung dieser Aufgabe reflektieren die Lernenden das Vorgehen bei der Addition von Brüchen. Hierfür wird GeoGebra verwendet, um eine statische bildliche Darstellung des Verfahrens zu liefern, das in formale Mathematik übersetzt werden muss.
Die bildliche Darstellung baut auf der Vorstellung von einem Bruch als Teil eines Ganzen auf. Sie ist nicht nur Teil der Aufgabe selbst, sondern auch Teil des Feedbackbereichs von STACK. Hier werden je nach Antwort der Lernenden Übersetzungen einzelner Schritte angezeigt, um die Lernenden zu aktivieren, sich den Rest selbst zu erarbeiten.
Nach einer gewissen Verzögerung wird eine ausführliche Lösung zugänglich gemacht.
Aufgabe 2 : Quadratische Gleichungen und Graphen
Gegenstand dieser Aufgabe ist die altbekannte Übersetzung eines algebraischen Ausdrucks in eine geometrische Abbildung.
Hier bietet GeoGebra ein interaktives Applet sowohl in der STACK-Aufgabe als auch im Feedback. Letzteres erfolgt in drei Schritten, jeweils nach einer gewissen Verzögerung:
-
Zuerst ermöglicht es den Lernenden, ihre falsche Lösung mit der richtigen zu vergleichen, was Fortgeschrittenen unmittelbar Hinweise auf den Fehler gibt, der vermutlich versehentlich gemacht wurde
- Für diejenigen, die mehr Hilfestellungen benötigen, bietet es eine interaktive Version der Situation in Kombination mit Fragen, die die Lernenden dabei unterstützen, sich selbst zu erarbeiten, wie der algebraische Ausdruck mit dem Graphen zusammenhängt.
- Schließlich wird eine Musterlösung zugänglich gemacht, die allen Lernenden gerecht wird, die eine schrittweise Anleitung benötigen, um Aufgaben dieser Art zu lösen.
Aufgabe 3 : Ein Bruch als Teil eines Ganzen
Diese Aufgabe, die man aus diversen Schulbüchern kennt, stellt einen Bruch als Teil eines Ganzen dar.
Während jedoch gedruckte Bücher "von Natur aus" statisch sind, ermöglicht GeoGebra hier einen dynamischen und interaktiven Zugang, der im Rahmen einer STACK-Aufgabe randomisiert ist. Wenn man die Aufgabe falsch macht, ist die erste Rückmeldung nur ein Hinweis. Wenn einem dieser ausreicht, kann man die Aufgabe mit neuen Werten wiederholen. Oder man wartet auf die Musterlösung.
Ein Spezialfall ist, dass der Lernende einen Bruch eingibt, der äquivalent zur erwarteten Lösung ist. Hier erhält er die Rückmeldung, dass er die Aufgabe nicht nach dem durch die Darstellung naheliegenden Schema bearbeitet, aber möglicherweise eine interessante Entdeckung gemacht hat...
Versuchen Sie unten diese Aufgaben.Loggen Sie sich ein oder erzeugen Sie einen Account, falls nötig.
-
-
-
Aufgabe 1: Winkel als rechten Winkel erzeugen
Bei dieser Aufgabe sollen die Lernenden darüber nachdenken, wann zwei Liniensegmente senkrecht zueinander sind. Sie müssen dann ihr Verständnis dieses Fachbegriffs mit dem Kreissatz und der Umkehrung des Kreissatzes in Verbindung bringen. GeoGebra wird zur visuellen Darstellung verwendet, und die Position des Punktes \(P\) stellt die Antwort des Schülers dar.
Bei diesem Problem wird die Position der Punkte \(A\) und \(B\) zufällig generiert.
Aufgabe 2: Erstellen Sie eine Funktion, indem Sie ihren Graphen skizzieren.
Diese Aufgabe fordert die Lernenden auf, über den Bereich und die Domäne einer Funktion nachzudenken. Sie können ihr Verständnis dieser Begriffe durch Skizzieren des Graphen einer Funktion demonstrieren.
GeoGebra wird verwendet, um den Graphen einer einfachen stückweisen Funktion visuell darzustellen, und die Position der vier Punkte auf dem Arbeitsblatt definieren die Enden der Funktionssegmente.
Diese Aufgabe bietet einen Ausgangspunkt für eine ganze Reihe ähnlicher Probleme, die die Eigenschaften von Funktionen untersuchen.
Aufgabe 3: Veranschaulichen Sie die Lage der Eigenvektoren
Diese Aufgabe stammt aus der fortgeschrittenen Mathematik auf Universitätsniveau. Eigenvektoren ist ein technischer Begriff für Vektoren, die durch eine Transformation skaliert werden, aber in der gleichen Richtung (oder in umgekehrter Richtung) bleiben. Das Verständnis für die Wirkung von Transformationen durch die Berechnung von Eigenvektoren ist ein wichtiges Thema in Vektorräumen.
Die Schüler werden sehr geschickt darin, Eigenvektoren durch ein mechanisches Verfahren zu berechnen, aber ihr geometrisches Verständnis bleibt oft lückenhaft.
GeoGebra is used to provide a visual representation of the vectors.
Im Prinzip könnte dieses Problem auf eine breitere Palette von 2D-Transformationen ausgedehnt werden.
Versuchen Sie unten diese Aufgaben.Loggen Sie sich ein oder erzeugen Sie einen Account, falls nötig.>
-
-
-
Aufgabe 1: Würfel
Diese Aufgabe befasst sich mit einem weit verbreiteten Irrtum, auch unter angehenden Lehrkräften, dass zwei Figuren auch die gleiche Oberfläche haben müssten, weil sie das gleiche Volumen haben. Das gegebene Beispiel zeigt den Lernenden erstens, dass zwei Figuren mit gleichem Volumen tatsächlich unterschiedliche Oberflächen haben können. Zweitens reflektieren die Studierenden das Potenzial ihrer eigenen Lernerfahrungen für den Unterricht ihrer zukünftigen Schülerinnen und Schüler.
Da es sich um eine einmalige Lerngelegenheit handelt, ist diese Aufgabe nicht randomisiert. GeoGebra wurde hier verwendet, um das Drehen der Figuren zu ermöglichen. Diese Aufgabe zur Reflexion der didaktischen Potenziale des eigenen Lernfortschritts ist Teil eines laufenden Forschungsprojekts an der UC.
Aufgabe 2: Flächeninhalt
Ähnlich wie die vorige Aufgabe bietet auch diese Aufgabe die Möglichkeit, über das didaktische Potenzial des eigenen Lernfortschritts nachzudenken.
Die Abbildung zeigt den ersten Teil der Aufgaben, bei dem die Studierenden den Flächeninhalt von zwei Figuren aus Tangramteilen vergleichen sollen, ohne eine Maßeinheit zu verwenden. Sie verwenden ein Applet, mit dem sie die Teile des einen Bildes auf das andere legen können, um so zu zeigen, dass beide Figuren die gleiche Fläche, aber unterschiedliche Formen haben.
Im zweiten Teil dieser Aufgabe müssen sie eine andere Strategie anwenden, nämlich das kleine Dreieck des Tangrams als Maßeinheit für einen indirekten Vergleich der beiden Flächen zu nehmen. Mit dieser Aufgabe sind sie in der Lage, die Unabhängigkeit zwischen der Fläche einer Figur und ihrer Form zu erklären.Aufgabe 3: Lineare Gleichungen
Diese Aufgabe macht keinen Gebrauch von GeoGebra. Stattdessen konzentriert sie sich auf die Erkundung der Möglichkeit von STACK, differenziertes, adaptives Feedback für ein einfaches algebraisches Problem bereitzustellen. Das Hauptaugenmerk liegt daher auf formativen Kommentaren, die sich jeweils auf einen spezifischen Fehler beziehen, den die SchülerInnen machen können.
Das gezielte Eingehen auf Fehler ermöglicht es den Lernenden, sich auf deren Korrektur zu konzentrieren und aus der Erfahrung zu lernen, so dass sie weniger Schwierigkeiten mit dem Thema haben.
Versuchen Sie unten diese Aufgaben.Loggen Sie sich ein oder erzeugen Sie einen Account, falls nötig.
-
-
-
Aufgabe 1: Faktorisieren I
Die folgenden zwei Aufgaben sind als zwei Schritte in einer Lernsequenz zu sehen. Ziel dieser Aufgabe ist es, die Faktorisierung des Quadrates eines Binoms einzuführen.
Wenn die Schüler eine falsche Antwort eingeben, erhalten sie eine Rückmeldung in Form eines interaktiven GeoGebra-Applets. Es zeigt ein Quadrat, das aus vier Rechtecken zusammengesetzt ist, die eine äquivalente Struktur des gegebenen algebraischen Ausdrucks darstellen. Der Schüler kann interaktiv erforschen, wie die Längen des Quadrats und seine strukturierte Fläche zusammenhängen, und so eine Strategie zur Faktorisierung quadrierter Binome herausfinden.
Aufgabe 2: Faktorisieren II
In dieser zweiten Aufgabe zur Faktorisierung geht es nun darum, die Faktorisierung eines allgemeinen quadratischen Ausdrucks einzuführen.
Beim Feedback zu falschen Antworten haben die Schülerinnen und Schüler erneut die Möglichkeit, mit einer geometrischen Figur zu interagieren, die ihnen hilft, eine Strategie zur Faktorisierung von Polynomen selbst herauszufinden. Anders als in der obigen Aufgabe ist das Objekt der Untersuchung nun ein Rechteck.
Aufgabe 3: Dreieck mit gegebenem Flächeninhalt
Ziel der Aufgabe ist es, dass die Lernenden die Formel für den Flächeninhalt eines Dreiecks anwenden und feststellen, dass Dreiecke mit gleicher Basis und gleicher Höhe unabhängig von der Form den gleichen Flächeninhalt haben. Die Lernenden werden entdecken, dass es mehrere Dreiecke gibt, die mit einem bestimmten Flächeninhalt gebildet werden können.
Es gibt zwei allgemeine Lösungsstrategien für diese Aufgabe. Erstens kann der Schüler die Fläche A mit 2 multiplizieren und dann die Basis und die Höhe finden, deren Produkt 2A ist. Zweitens kann der Schüler ein Rechteck mit den Maßen b x h verwenden und dann eine der Seiten als Basis verwenden und den dritten Punkt auf die gegenüberliegende Seite legen.
Versuchen Sie unten diese Aufgaben.Loggen Sie sich ein oder erzeugen Sie einen Account, falls nötig.
-
